实时称重卡尔曼滤波：精确测量的关键技术

引言

在工业自动化和智能交通等领域，实时称重系统扮演着至关重要的角色。它不仅能够提供精确的重量数据，还能实时监测重量变化，对于质量控制和物流管理具有重要意义。卡尔曼滤波作为一种高效的信号处理技术，被广泛应用于实时称重系统中，以实现高精度和稳定性。本文将深入探讨实时称重卡尔曼滤波的原理、实现方法及其在实际应用中的优势。

卡尔曼滤波简介

卡尔曼滤波是一种线性、时不变的递归滤波算法，由美国科学家鲁道夫·卡尔曼于1960年提出。它能够从一系列观测数据中估计出系统的状态，并具有以下特点：

• 线性化处理：将非线性系统通过线性化方法转化为线性系统，便于计算。
• 最小均方误差：在所有线性无偏估计中，卡尔曼滤波器能够最小化估计误差。
• 递归计算：只需保存有限个历史数据，即可实现实时估计。

实时称重卡尔曼滤波原理

实时称重系统通常由传感器、信号处理单元和执行机构组成。在信号处理单元中，卡尔曼滤波器负责对传感器采集到的重量数据进行处理，以实现精确的重量估计。

1. 状态空间模型

实时称重卡尔曼滤波器首先建立状态空间模型，将重量视为状态变量。状态空间模型由以下三个部分组成：

• 状态方程：描述系统状态变化的方程，如 ( x_{k+1} = Fx_k + Bu_k )，其中 ( x_k ) 为状态向量，( F ) 为状态转移矩阵，( u_k ) 为控制向量。
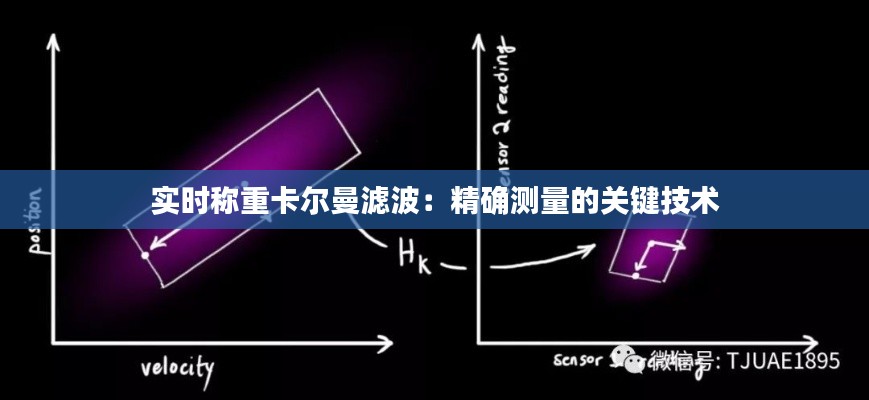
• 观测方程：描述系统状态与观测数据之间的关系，如 ( z_k = Hx_k + v_k )，其中 ( z_k ) 为观测数据，( H ) 为观测矩阵，( v_k ) 为观测噪声。
• 初始状态：描述系统初始时刻的状态，如 ( x_0 )。

2. 卡尔曼滤波器算法

卡尔曼滤波器算法主要包括以下步骤：

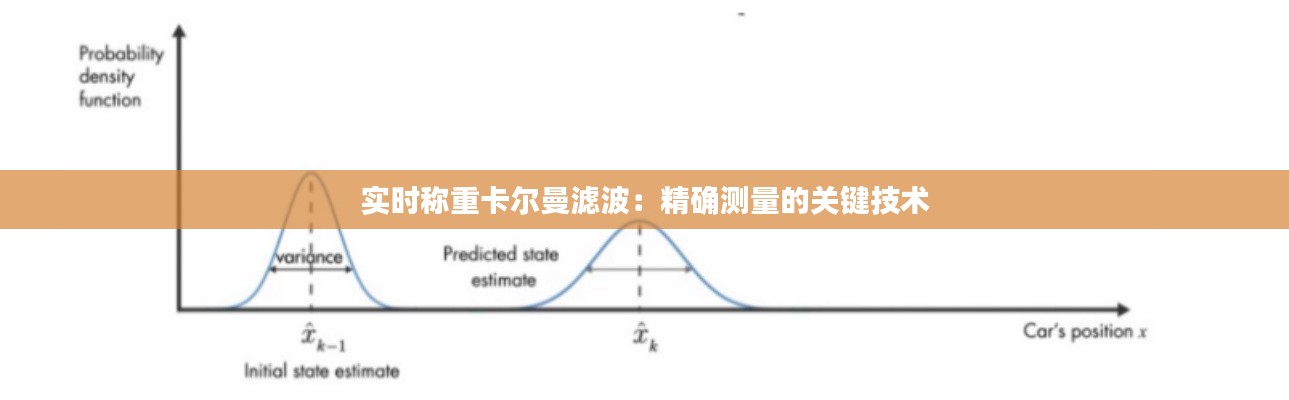
• 预测：根据上一时刻的状态估计当前时刻的状态，如 ( \hat{x}k|{k-1} = F\hat{x}{k-1}|{k-1} + B\hat{u}_k )。
• 更新：结合观测数据对预测状态进行修正，如 ( \hat{x}_k|_k = \hat{x}k|{k-1} + K_k(z_k - H\hat{x}k|{k-1}) )，其中 ( K_k ) 为卡尔曼增益。
• 估计误差协方差：更新估计误差协方差矩阵，如 ( Pk = FP{k-1}F^T + Q_k )，其中 ( P_k ) 为估计误差协方差矩阵，( Q_k ) 为过程噪声协方差矩阵。

实时称重卡尔曼滤波实现

实时称重卡尔曼滤波的实现主要包括以下步骤：

• 传感器数据采集：通过传感器获取实时重量数据。
• 数据预处理：对采集到的数据进行滤波、去噪等预处理操作。
• 卡尔曼滤波器初始化：根据系统特性设置状态空间模型参数、初始状态、初始误差协方差等。
• 卡尔曼滤波器迭代：根据卡尔曼滤波器算法进行迭代计算，得到实时重量估计值。

实际应用优势

实时称重卡尔曼滤波在实际应用中具有以下优势：

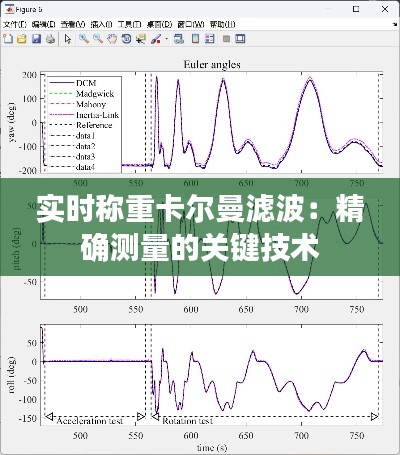
• 高精度：卡尔曼滤波器能够有效降低观测噪声和系统噪声的影响，提高重量估计精度。
• 实时性：卡尔曼滤波器采用递归计算，能够实时更新重量估计值。
• 稳定性：卡尔曼滤波器能够适应系统状态变化，保持估计精度稳定。

结论

实时称重卡尔曼滤波作为一种高效、稳定的信号处理技术，在实时称重系统中具有广泛的应用前景。通过本文的探讨，我们了解了卡尔曼滤波的原理、实现方法及其在实际应用中的优势。随着技术的不断发展，实时称重卡尔曼滤波将在更多领域发挥重要作用。